Bạn đang tìm hiểu về các công thức đạo hàm, từ đạo hàm cơ bản đến đạo hàm cấp cao thì đây chính là một bài viết dành trọn cho bạn. Cụ thể công thức đạo hàm như thế nào, hãy xem ngay dưới đây nhé!
1 Đạo Hàm là gì?
Trước hết, chúng ta hãy tìm hiểu xem đạo hàm là gì nhé!
Đạo hàm được định nghĩa theo 3 loại là Giải Tích ,Hình Học và Vật Lý.Cụ thể:

1.1 Đạo hàm trong giải tích
Đạo hàm của một hàm số thực chất là sự mô tả sự biến thiên của hàm số tại một điểm nào đó.
1.2 Đạo hàm trong hình học
Đạo hàm trong hình học là hệ số góc của tiếp tuyến với đồ thị biểu diễn hàm số.
Nếu tồn tại, f′(x0)f′(x0) là hệ số góc của tiếp tuyến của đồ thị hàm số y=f(x)y=f(x) tại điểm M0(x0;f(x0))M0(x0;f(x0)).
Khi đó phương trình tiếp tuyến của đồ thị tại điểm M0(x0;f(x0))M0(x0;f(x0)) là
y−f(x0)=f′(x0)(x−x0)
1.3 Đạo hàm trong Vật Lý
Trong vật lý, đạo hàm là vận tốc tức thời của một chất điểm chuyển động hoặc cường độ dòng điện tức thời tại một điểm trên dây dẫn.
v(t)=s′(t)v(t)=s′(t) là vận tốc tức thời của chuyển động s=s(t)s=s(t) tại thời điểm tt.
2 Định nghĩa Đạo Hàm
Cho hàm số y=f(x)y=f(x) xác định trên khoảng (a;b)(a;b), x0∈(a;b)x0∈(a;b).
3 Quy tắc của đạo hàm
4 Quan hệ giữa tính liên tục và sự tồn tại đạo hàm
Định lí. Nếu hàm số y=f(x)y=f(x) có đạo hàm tại x0x0 thì nó liên tục tại x0x0.
Chú ý.
Định lí trên tương đương với khẳng định : Nếu y=f(x)y=f(x) gián đoạn tại x0x0 thì nó không có đạo hàm tại điểm đó.
Mệnh đề đảo của định lí không đúng. Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.
5 Quy tắc tính đạo hàm
6 Đạo Hàm của hàm số lượng giác
(sinx)’ = cosx
6.1. Giới hàn của sinxxsinxx
Thừa nhận định lý: limx→0sinxx=1limx→0sinxx=1
6.2. Đạo hàm của hàm số lượng giác
+ Hàm số y=sinxy=sinx có đạo hàm ∀x∈R∀x∈R và (sinx)′=cosx(sinx)′=cosx ;
+ Hàm số y=cosxy=cosx có đạo hàm ∀x∈R∀x∈R và (cosx)′=−sinx(cosx)′=−sinx;
+ Hàm số y=tanxy=tanx có đạo hàm ∀x≠π2+kπ,k∈∀x≠π2+kπ,k∈ và (tanx)′=1cos2x(tanx)′=1cos2x;
+ Hàm số y=cotxy=cotx có đạo hàm ∀x≠kπ,k∈∀x≠kπ,k∈ và (cotx)′=−1sin2x(cotx)′=−1sin2x
6.3. Bảng tổng hợp đạo hàm của hàm số lượng giác
| (sinx)′=cosx(sinx)′=cosx | (sinu)′=(cosu).u′=u′.cosu(sinu)′=(cosu).u′=u′.cosu |
| (cosx)′=−sinx(cosx)′=−sinx | (cosu)′=(−sinu).u′=−u′.sinu(cosu)′=(−sinu).u′=−u′.sinu |
| (tanx)′=1cos2x(tanx)′=1cos2x | (tanu)′=u′cos2u(tanu)′=u′cos2u |
| (cotx)′=−1sin2x(cotx)′=−1sin2x | (cotu)′=−u′sin2u |
Xem thêm:
- Công thức tính diện tích và thể tích khối nón kèm 4 ví dụ hay
- Công thức tính diện tích tam giác vuông, đều, cân, vuông cân chuẩn
- Tổng hợp các công thức tính công suất và 5 ví dụ chuẩn
- Hướng dẫn cách tính công suất điện 3 pha chuẩn
7 Công thức Đạo hàm cơ bản
Bảng đạo hàm các hàm số đa thức, hàm số lượng giác, hàm số mũ và hàm số logarit cơ bản biến x.
| Bảng đạo hàm các hàm số cơ bản |
| (xα)’ = α.xα-1 |
| (sin x)’ = cos x |
| (cos x)’ = – sin x |
| (tan x)’ = 1cos2x = 1 + tan2 x |
| (cot x)’ = −1sin2x = -(1 + cot2 x) |
| (logα x)’ = 1x.lnα |
| (ln x)’ = 1x |
| (αx)’ = αx . lnα |
| (ex)’ = ex |
8 Công thức đạo hàm các hàm số nâng cao
Bảng đạo hàm các hàm số đa thức, hàm số lượng giác, hàm số mũ và hàm số logarit của một hàm số đa thức u = f(x).
| Bảng đạo hàm các hàm số nâng cao |
| (uα)’ = α.u’.uα-1 |
| (sin u)’ = u’.cos u |
| (cos u)’ = – u’.sin u |
| (tan u)’ =
u′cos2u = u'(1 + tan2 u) |
| (cot u)’ =
−usin2u = -u'(1 + cot2 x) |
| (logα u)’ =
uu.lnα |
| (ln u)’ =
u′u |
| (αu)’ = u’.αu.lnα |
| (eu)’ = u’.eu |
9 Công thức đạo hàm lượng giác
10 Công thức đạo hàm cấp 2
Hàm số y = f(x) có đạo hàm tại x ∈ (a; b).
Khi đó y’ = f'(x) xác định một hàm sô trên (a;b).
Nếu hàm số y’ = f'(x) có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) tại x.
Kí hiệu: y” hoặc f”(x).
Ý nghĩa cơ học:
Đạo hàm cấp hai f”(t) là gia tốc tức thời của chuyển động S = f(t) tại thời điểm t.
11 Công thức đạo hàm cấp cao
Cho hàm số y = f(x) có đạo hàm cấp n-1 kí hiệu f (n-1) (x) (n ∈ N, n ≥ 4).
Nếu f (n-1) (x) có đạo hàm thì đạo hàm của nó được gọi là đạo hàm câp n của y = f(x), y (n) hoặc f (n) (x).
f (n) (x) = [f (n-1) (x)]’
Công thức đạo hàm cấp cao:
(x m)(n) = m(m – 1)(m – 2)…(m – n + 1).xm – n (nếu m ≥ n)
(x m)(n) = 0 (nếu m ≤ n)
Tổng kết
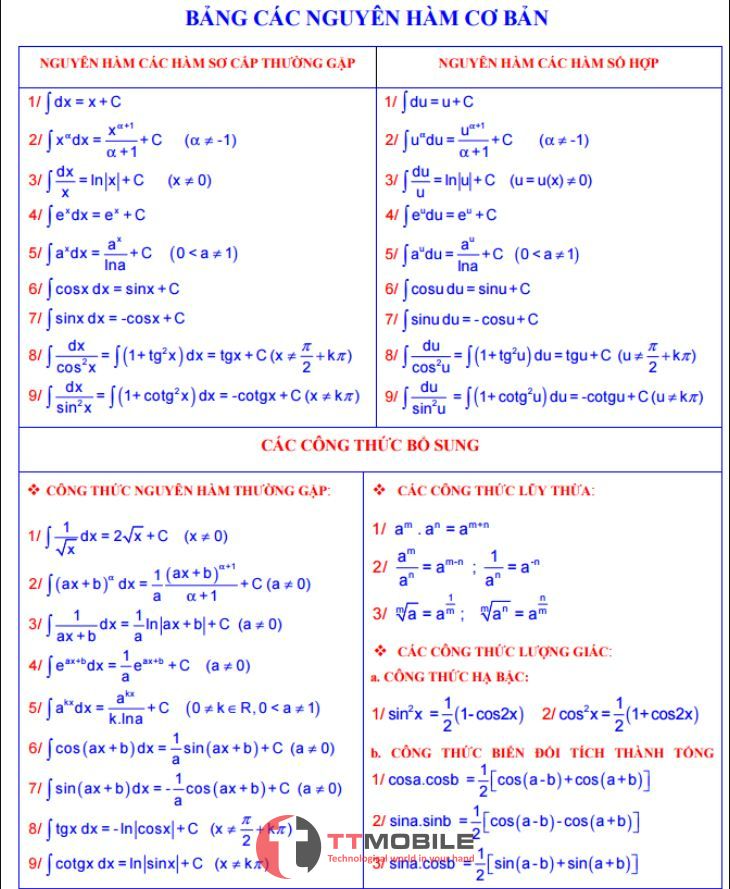
12 Công thức đạo nguyên hàm
13 Công thức đạo hàm 2 biến
Đạo hàm của hàm hai biến, luôn phải chia 2 trường hợp: đạo hàm theo x hoặc đạo hàm theo y. Khi lấy đạo hàm theo biến nào thì biến kia giữ vai trò là hằng số.
Hàm 2 biến có 4 đạo hàm cấp 2, đạo hàm cấp 2 theo biến x, đạo hàm cấp 2 theo biến y, đạo hàm cấp 2 hỗn hợp xy và đạo hàm cấp 2 hỗn hợp yx.
Đạo hàm cấp 2 theo biến x được lấy từ đạo hàm cấp 1 theo biến x một lần nữa theo x.
Đạo hàm cấp 2 theo biến y được lấy từ đạo hàm cấp 1 theo biến y một lần nữa theo y.
Đạo hàm cấp 2 hỗn hợp xy được lấy từ đạo hàm cấp 1 theo biến x một lần nữa theo y.
Đạo hàm cấp 2 hỗn hợp yx được lấy từ đạo hàm cấp 1 theo biến y một lần nữa theo x.
Vì vậy, Ta có tính chất: đạo hàm cấp 2 hỗn hợp bằng nhau,
tức là: f_xy = f_yx
Trên đây là tổng hợp các công thức đạo hàm từ cơ bản đến nâng cao xin gửi đến bạn đọc.Còn một số công thức nữa sẽ được cập nhật thêm.Chúc các bạn cập nhật được những kiến thức cần thiết cho mình. Rất cảm ơn bạn đã quan tâm và đọc bài.