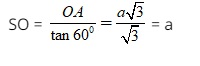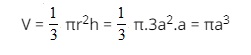Công thức tính diện tích và thể tích khối nón kèm 4 ví dụ hay

Hình khối được thể hiện và bắt gặp trên những trang giấy của học sinh là vô cùng nhiều. Vì sao các hình khối lại được cho vào một chương giảng dạy quan trọng trong chương trình học Trung học Phổ thông? Chính là vì các áp dụng thực tiễn của hình khối xuất hiện rất nhiều trong đời sống và ta có thể dễ dàng bắt gặp từ những điều nhỏ nhất như: hộp sữa, quả bóng,… hoặc vĩ mô hơn là công trình kiến trúc Kim Tự Tháp – Ai Cập. Vì có tính ứng dụng khá cao trong đời sống nên một số hình khối phổ biến xuất hiện trong giảng dạy như: hình khối lập phương, hình khối trụ, hình khối chóp, hình khối nón,… Bài viết sau đây sẽ giúp bạn ôn lại một số kiến thức ở trung học phổ thông nhé. Bây giờ chúng mình sẽ tìm hiểu về thể tích của 1 loại hình khối rất quen thuộc đó chính là thể tích hình khối nón.

Khối nón là hình gì? 

Trước khi đi đến công thức tính diện tích cũng như thể tích khối nón ta sẽ cùng đi tìm hiểu  qua về định nghĩa và cấu tạo của chúng một chút.

Định nghĩa mặt nón? 

Hình mặt nón

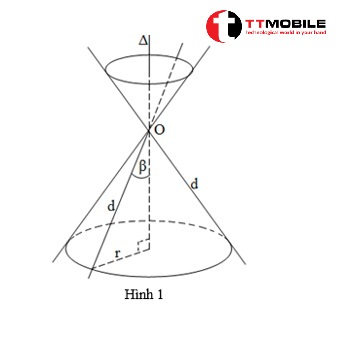
Cho 2 đường thẳng d và Δ cắt nhau tại giao điểm O, cùng năm trong một mặt phẳng (P). Chúng giao nhau và tạo thành một góc β không đổi, khi đó, 0 < β < 900. 

Mặt tròn xoay khi này tạo ra bởi đường thẳng d khi quay xung quanh O được gọi mà mặt nón hoặc ta có thể hiểu khi quay mặt phẳng (P) xung quanh trục của đường thẳng d cùng góc β không thay đổi tại giao điểm O ta được một mặt nón tròn xoay với đỉnh của nó là đỉnh O ( hình 1 ).

Mặt nón tròn xoay thường được gọi tắt là mặt nón.

Trong đó:

• Trục của mặt nón là đường thẳng Δ
• Đường sinh của mặt nón là đường thẳng d
• Đỉnh của mặt nón tròn xoay là O
• Góc đỉnh của mặt nón là 2β

Sau khi ta định nghĩa được mặt nón, muốn biết thể tích khối nón ta phải tìm hiểu thêm về định nghĩa hình khối nón.

Tham khảo thêm các công thức khác :

• Công thức tính diện tích tam giác vuông, đều, cân, vuông cân chuẩn
• Tổng hợp các công thức tính công suất và 5 ví dụ chuẩn
• Hướng dẫn cách tính công suất điện 3 pha chuẩn

Định nghĩa hình nón và khối nón tròn xoay:

Hình khối nón tròn

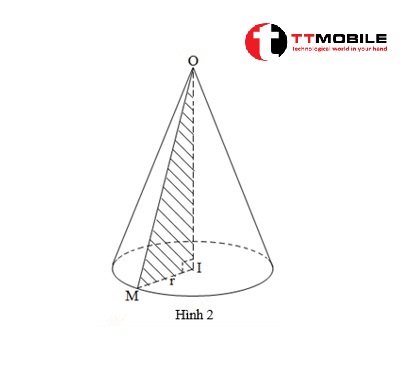
Cho một ΔOIM vuông tại I. Chọn đường thẳng cạnh góc vuông OI làm tâm và quay cạnh huyền OM xung quanh đường thẳng OI đó, ta tạo được một hình ( hình 2 ), gọi là hình nón tròn xoay hoặc ta có thể gọi là khối nón.

Trong đó: 

• Đường thẳng OI được gọi là trục khối nón.
• gọi là đỉnh của hình khối nón.OI chính là đường cao của khối nón.
• OM được gọi là đường sinh của hình khối nón.I là tâm của hình tròn ( đáy của khối nón ).
• Bán kính hình tròn r ( đáy của khối nón ) là IM.

Định nghĩa xong mặt nón tròn xoay, hình nón và khối nón, ta bắt đầu đi đến tìm hiểu về diện tích khối nón, thể tích khối nón. 

Diện tích khối nón, thể tích khối nón:

Diện tích khối nón, thể tích khối nón:

Cho một khối nón có L là đường sinh, h là đường cao và bán kính đáy là R, ta có:

Diện tích xung quanh : 

Diện tích xung quanh khối nón bằng tích của số pi với tích của bán kính đáy và đường sinh.

Sxq  =  πRL

Diện tích đáy ( hình tròn ) :

Diện tích đáy (hình tròn) khôi nón bằng tích của số pi với bình phương bán kính đáy.

Sđ  = πR2

Diện tích toàn phần hình khối nón:

Diện tích toàn phần hình khối nón được xác định bằng tổng diện tích xung quanh và diện tích đáy (hình tròn).

S  =  Sxq  +  Sđ  =   πRL  +  πR2

Thể tích khối nón :

Thế tích khối nón được xác định tính toán bằng công thức tích của 1 phần 3 với đường cao, bình phương bán kính đáy (hình tròn) và số pi.

Vnón   =  13.h. π. R2 

Tính chất: 

Từ các định nghĩa về mặt nón tròn xoay, hình nón, khối nón và các công thức tính diện tích, thể tích khối nón ta có một số tính chất của hình khối nón như sau:

• Nếu một mặt phẳng đi ngang qua đỉnh và cắt mặt nón tròn xoay thì xảy ra các trường hợp sau đây: 

Thiết diện của hình nón là tam giác cân nếu mặt phẳng cắt mặt nón theo 2 đường sinh.

Người ta gọi là mặt phẳng tiếp diện của mặt nón trong trường hợp mặt phẳng tiếp xúc với mặt nón theo một đường sinh.

• Nếu một mặt phẳng cắt mặt nón tròn xoay nhưng lại không đi qua đỉnh thì có các trường hợp sau xảy ra:

Giao tuyến là một đường tròn xuất hiện khi mặt phẳng cắt vuông góc với trục hình nón.

Giao tuyến là 2 nhánh của 1 hypebol Nếu mặt phẳng cắt song song với 2 đường sinh hình nón.

Giao tuyến là 1 đường parabol nếu như mặt phẳng cắt song song với 1 đường sinh hình nón.

Một số ví dụ tính diện tích khối nón, thể tích khối nón:

Ví dụ minh họa 1:

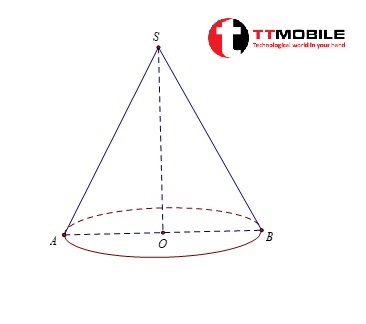
Cho hình khối nón có chiều cao là 6a và bán kính đáy là 8a. Tính đường sinh, diện tích đáy, diện tích xung quanh, diện tích toàn phần và thể tích khối nón trên.

Công thức tính thể tích khối nón

Xét tam giác SOB, ta có: 

h = SO = 6a

R = OB = 8a

Độ dài đường sinh là :

L = SA = SO2 + OB2  = 6a2+8a2  = 10a

Diện tích đáy khối nón là:

Sđ   =  πR2   =  π. 8a2  = 64πa2

Diện tích xung quanh khối nón là:

Sxq  =  πRL  =  π. 8a. 10a  =  80πa2

Diện tích toàn phần khối nón là: 

S  =  Sxq  +  Sđ  =   80πa2  +  64πa2  =  144πa2

Thể tích khối nón là: 

Vnón   =      13 h.π.R2   =     13 . 6a. π. 8a2  =  16πa3

 

Ví dụ minh họa 2: 

Cho một khối nón có thể tích khối nón bằng 30 π, nếu tăng bán kính khối nón đó lên 2 lần và giữ nguyên chiều cao thì thể tích của khối nón mới tạo bằng bao nhiêu?

Ta gọi V1  =   13. h. π. R2   là thể tích khối nón lúc đầu là:

→ Công thức tính thể tích khối nón sau khi tăng 2 lần chiều cao là:

V2  =  13. h. π. (2R)2  =  43. h. π. R2  = 4V1

V2  = 4. 30π  =  120π

 

Ví dụ minh họa 3 :

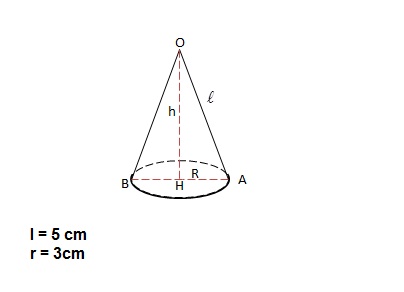
Cho khối nón như hình vẽ trên có độ dài đường sinh bằng 5cm, bán kính hình tròn đáy là 3cm. Tính thể tích khối nón

Lời giải :

Như đề bài ta có dữ liệu l = 5cm , r = 3 cm

 

 

 

 

 

 

Đáp án V = 12π (cm)³ .

 

Ví dụ minh họa 4 :

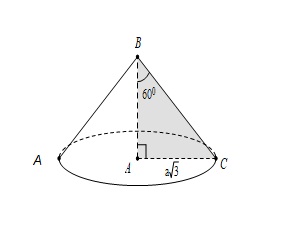
Một hình nón có đường kính đáy là 2a√3 , góc ở đỉnh là 120 độ. Tính thể tích của khối nón đó theo a.

Lời giải:

Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.

Theo giả thiết dễ suy ra đường tròn đáy có bán kính là:

Xét tam giác SAO vuông tại O, ta có:

Do đó chiều cao hình nón là h = SO= a.

Vậy thể tích khối nón là

Áp dụng của hình khối, công thức tính diện tích và thể tích hình khối tỏng đời sống, giảng dạy:

Toán học là một ngành khoa học mang tính trừu tượng cao và đối với các hình khối nói chung và hình khối nón nói riêng đều mang tính đặc tính trừu tượng của ngành khoa học này. 

Mặc dù mang tính trừu tượng cao nhưng không thể phủ bỏ vai trò những công thức tính toán chiều dài, chu vi, diện tích, thể tích của các hình khối nói chung và các diện tích, thể tích khối nón nói riêng lại rất quan trọng trong cuộc sống, nhất là trong các công trình xây dựng kỹ thuật, công nghệ, hạ tầng hay cơ sở vật chất nói chung.

Hình học không gian áp dụng nhiều vào thực tế

Bên cạnh những áp dụng thực tiễn của công thức tính tính chiều dài, độ cao, diện tích và thể tích khối nón vừa được đề cập ở trên thì toán học là một trong ba môn học được chú trọng nhất trong chường trình giảng dạy của tất cả các cấp học trong chương tình dạy học của bộ giáo dục. Từ đó, ta có thể thấy được tầm quan trọng của toán học, không chỉ vô tình hay tự nhiên mà nó trở thành môn học chính của tất cả các cấp.

Nhưng ở đây, ta cũng nhận thấy được một số bất cập trong phương pháp giảng dậy trong nhà trường như các công thức tính toán nói chung và công thức tính diện tích, thể tích khối nón nói riêng được đưa vào giảng dạy một cách rập khuôn và cứng nhắc.

Cho đến vài năm trở lại đây, khi bộ giáo dục đã có một số bước tiến, cải cách chương trình học mới, những câu đố, đề bài mình họa đã bắt đầu thể hiện được khía cạnh thực tiễn, thực tế của toán học. Đây chính là dấu hiệu đáng mừng cho ngành khoa học này tại Việt Nam.