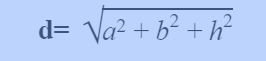Cách tính thể tích khối nón, khối trụ và thể tích hình hộp chữ nhật

Toán học có vị trí vô cùng quan trọng trong cuộc sống, đặc bị là hình học vì tính ứng dụng vào thực tế vô cùng cao. Căn nhà, khu vườn, hồ bơi,… muốn tính diện tích, thể tích để xây dựng thì đều cần tới hình học. Vậy cách tính, công thức tính thể tích khối nón, khối trụ, thể tích hình hộp chữ nhật,… chính xác như thế nào? Hãy bớt chút thời gian tham khảo bài viết này để nhớ lại các công thức này nhé.

Cách tính thể tích khối nón

Tổng quan về khối nón 

Toán học gồm có phần đại số và phần hình học. Trong chương trình hình học thì có hình học phẳng và hình học không gian. Phần hình học thường trừu tượng và thú vị hơn so với phần đại số vì đối với phần hình học không gian có thể giúp chúng ta hình dung được hình ảnh qua không gian ba chiều ở những phần bị che khuất, không được thể hiện trên hình học phẳng. 

Khối nón trong toán học 

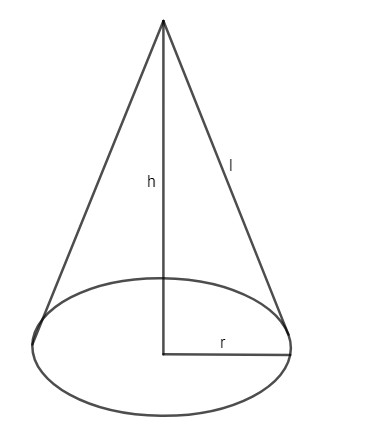
Chương trình đề cập đến nhiều hình, trong đó có khối nón hay còn gọi là hình nón. Khối nón là hình học vô cùng quen thuộc với chúng ta vì nó xuất hiện phổ biến trong nhiều lĩnh vực như: dù, nón lá,.. Vậy khối nón trong toán học là gì? Khối nón là khối hình được tạo thành khi thực hiện xoay một vòng 360 một tam giác vuông quanh trục của nó chính là một cạnh góc vuông thì ta thu được khối nón. Cũng chính vì đặc điểm thế mà khối nón là phần không gian được giới hạn bởi không gian xung quanh tạo bởi đường sinh và mặt đáy.

Đặc điểm của khối nón

• Độ dài tính từ đỉnh nón đến tâm của hình tròn đáy là chiều cao của khối nón
• Bán kính của hình tròn đáy là bán kính của khối nón 
• Đường sinh của khối nón là độ dài cạnh huyền của tam giác quay 

Các công thức tính diện tích khối nón 

Để tính được diện tích của khối nón thì ta thực hiện tính diện tích xung quanh và diện tích toàn phần của hình nón đó. Trong đó, diện tích xung quanh của khối nón là phần không gian xung quanh của khối nón, diện tích xung quanh không bao gồm diện tích đáy.

Công thức tính diện tích xung quanh khối nón:

Sxungquanh = π.r.l

Trong đó:

• Sxungquanh là diện tích xung quanh của khối nón 
• r là bán kính của của hình tròn đáy
• l là độ dài đường sinh của khối nón.

Diện tích toàn phần của khối nón chính là bao gồm toàn bộ không gian hình nón chiếm giữ, gồm có diện tích đáy và diện tích xung quanh. Hay nói đơn giản thì diện tích toàn phần của khối nón là tổng của diện tích xung quanh với diện tích đáy khối nón.

Công thức tính diện tích toàn phần khối nón:

Stoanphan = πrl + πr2

Trong đó 

• Stoanphan là diện tích toàn phần của khối nón 
• r là bán kính của hình tròn đáy 
• l là độ dài của đường sinh 

Thể tích khối nón là toàn bộ phần không gian bên trong mà khối nón chiếm giữ.

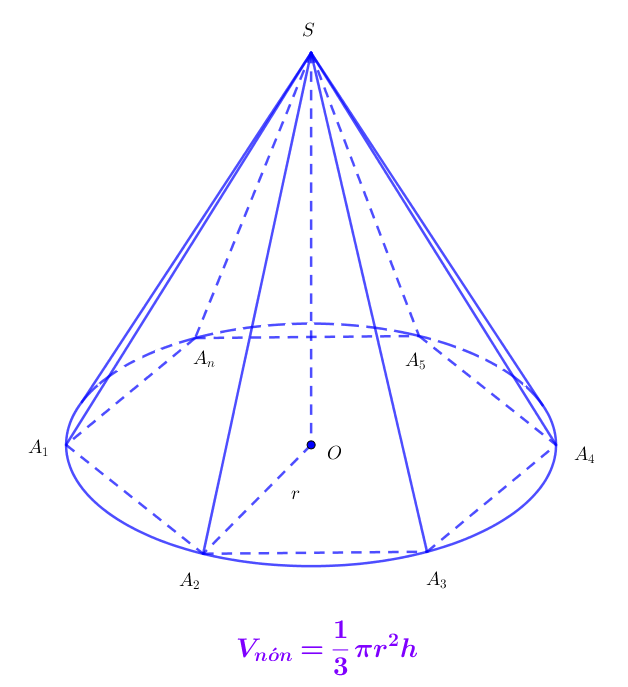
Công thức tính thể tích của khối nón bằng chiều cao của khối nón nhân với 1/3 diện tích của mặt đáy khối nón.

Trong công thức khối nón đó:

• V là thể tích của khối nón.
• r là bán kính đáy.
• h là chiều cao của khối nón , khoảng cách từ đỉnh của khối nón tới đáy.

Thể tích khối nón bao gồm toàn bộ không gian ben trong khối nón

Cách tính thể tích khối trụ 

Tổng quan về khối trụ 

Có rất nhiều vật dụng quen thuộc trong cuộc sống mang hình trụ tròn như: cốc nước, lon sữa đặc,… Từ đó có thể dễ dàng nhận ra hình trụ tròn là hình có hai mặt đáy là hai hình tròn song song với nhau và bằng nhau. Vì tính ứng dụng cao nên cách tính toán thể tích cũng như diện tích hình trụ được áp dụng rất nhiều trong thực tế. Khối trụ chính là không gian trong của hình trụ đó.

Thể tích khối trụ là gì

Định nghĩa hình trụ trong toán học chính là hình được giới hạn bởi mặt trụ và hai đường tròn bằng nhau, là giao tuyến của mặt trụ với hai mặt phẳng vuông góc với trục. Hình trụ chính là hình tròn xoay được tạo bởi 4 cạnh của hình chữ nhật khi tiến hành quay một góc 360 độ xung quanh một đường trung bình của hình chữ nhật đó.

Thể tích khối trụ trong toán học

Khối trụ có bản chất chính là hình trụ và phần bên trong của hình trụ đó. Thể tích của khối trụ được tính bằng tích của diện tích của mặt đáy cùng chiều cao hình trụ.

Các công thức tính thể tích khối trụ 

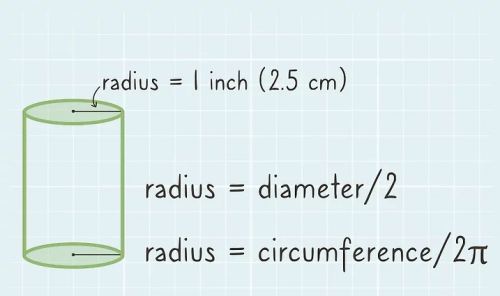
Tương tự như cách tính thể tích khối nón, muốn tính thể tích khối trụ, ta lấy chiều cao nhân với bình phương độ dài của bán kính hình tròn ở mặt đáy hình trụ và số pi. Công thức tính thể tích hình trụ: V = πR2.h.

Trong đó:

• V là thể tích khối trụ có đơn vị là mét khối (m3)
• r là bán kính hình tròn ở mặt đáy khối trụ có đơn vị là mét (m)
• h là chiều cao của khối trụ có đơn vị là mét (m)
• π là hằng số pi ( π = 3, 14)

Thể tích khối trụ bao gồm hình trụ và phần bên trong hình trụ 

Công thức tính diện tích, chu vi , thể tích hình hộp chữ nhật 

Tổng quan hình hộp chữ nhật 

Là một hình không gian gần gũi với cuộc sống của con người. Ta có thể thấy hình hộp chữ nhật ở mọi nơi như: hộp diêm, hộp đựng giày,… Định nghĩa hình hộp chữ nhật trong toán học là một hình không gian có 6 mặt đều là hình chữ nhật, có 8 đỉnh và 12 cạnh. Hai mặt của hình hộp chữ nhật song song với nhau và được gọi là các mặt đối diện.

Trong 6 mặt của hình hộp chữ nhật thì được chia làm 3 cặp mặt đối diện gồm có 1 cặp mặt đáy và 2 cặp mặt bên.

Nếu ta gọi 2 mặt bất kỳ đối diện nhau là mặt đáy, thì 4 mặt còn lại mà mặt bên của hình hộp chữ nhật.

Dấu hiệu nhận biết hình hộp chữ nhật

Dễ nhận biết hình hộp chữ nhật bởi hình có 12 cạnh, 8 đỉnh và 6 mặt.

Hình hộp chữ nhật có đường chéo có hai đầu mút là 2 đỉnh đối nhau và các đường chéo của hình hộp chữ nhật đồng quy tại một điểm

Hai mặt đối diện trong hình hộp chữ nhật có diện tích bằng nhau

Hai mặt đối diện trong hình hộp chữ nhật có chu vi bằng nhau

Các công thức về hình hộp chữ nhật

Chu vi hình hộp chữ nhật

Cách tính chu vi hình hộp, ta thwujc hiện tính tổng độ dài tất cả các cạnh bên và cạnh đáy của hình hộp chữ nhật.

Công thức:

P = (a+b+h).4

Trong đó:

• a là chiều dài hình hộp chữ nhật
• b  là chiều rộng hình hộp chữ nhật
• h  là chiều cao hình hộp chữ nhật

Diện tích xung quanh của hình hộp chữ nhật

Diện tích xung quanh hình hộp chữ nhật bằng tích của chu vi mặt đáy và chiều cao

Công thức tính:

Sxq= 2h.(a+b)

Trong đó:

• Chiều dài hình hộp chữ nhật: a
• Chiều rộng hình hộp chữ nhật: b
• Chiều cao hình hộp chữ nhật: c

Diện tích toàn phần của hình hộp chữ nhật

Muốn tính diện tích toàn phần của hình hộp chữ nhật ta thực hiện tính tổng diện tích 6 mặt của hình hộp chữ nhật đó. 

Chính vì vậy ta có công thức tính diện tích toàn phần hình hộp chữ nhật: bằng tổng diện tích xung quanh của hình hộp chữ nhật và 2 mặt còn lại. 

Stp= Sxq+S2 đáy

Hay Stp= 2h.(a+b) +2ab

Trong đó:

• Diện tích của hình hộp chữ nhật (diện tích xung quanh và diện tích toàn phần): S
• Chiều dài của hình hộp chữ nhật: a
• Chiều rộng của hình hộp chữ nhật: b
• Chiều cao của hình hộp chữ nhật: c

Công thức tính đường chéo hình hộp chữ nhật

Độ dài các đường chéo trong hình hộp chữ nhật bằng nhau. Công thức tính:

Công thức tính đường chéo hình hộp chữ nhật 

Trong đó:

• Đường chéo của hình hộp chữ nhật: d
• Chiều dài của hình hộp chữ nhật: a
• Chiều rộng của hình hộp chữ nhật: b
• Chiều cao của hình hộp chữ nhật: c

Công thức tính thể tích hình hộp chữ nhật 

Muốn tính thể tích hình hộp chữ nhật, ta lấy chiều dài hình hộp chữ nhật nhân với chiều cao và chiều rộng của hình hộp chữ nhật đó. 

Công thức tính thể tích hình hộp chữ nhật: V = a.b.h

Trong đó:

• Thể tích hình hộp chữ nhật: V
• Chiều dài hình hộp chữ nhật: a
• Chiều rộng hình hộp chữ nhật: b
• Chiều cao hình hộp chữ nhật: h

Công thức tính thể tích hình chữ nhật được áp dụng phổ biến trong cuộc sống, trong xây dựng vì hình hộp chữ nhật là hình được sử dụng nhiều trong các công trình như; hồ bơi, bể nước, diện tích bể chứa,…

Cách tính thể tích hình hộp chữ nhật được áp dụng nhiều trong cuộc sống 

Lời kết

Bài viết ngắn đã gửi đến các bạn một số công thức quan trọng trong hình học không gian và gắn liền với cuộc sống như: thể tích khối nón, thể tích khối trụ và các công thức tính toán xoay quanh hình hộp chữ nhật. Mong rằng qua bài viết này, chúng tôi đã giúp bạn thể hệ thống lại phần nào những kiến thức cơ bản đã học về hình học không gian và vận dụng linh hoạt vào những vấn đề cần thiết trong cuộc sống thường ngày. Chúc các bạn thành công.